TEMEL MATEMATİKSEL YAPILAR

Monoidler -- Gruplar -- Halkalar -- Cisimler -- Topolojik Uzaylar -- Manifoldlar -- Hilbert Uzayları -- Sıralamalar -- analitik geometri

Grup kuramı

Üzerinde tersinebilir ve bileşme özelliğine sahip ikili bir işlemin tanımlı olduğu kümelerin kuramıdır. Daha detaylı açıklamak gerekirse, grup nesnesi bir küme G ve onun üzerinde tanımlı bir $cdot$ işleminden oluşur. Bu operasyonun aşağıdaki şartları sağlaması gereklidir:

1) G'nin herhangi üç elemanı a,b,c için

$acdot(bcdot c)=(acdot b)cdot c$

eşitliği sağlanmalıdır,

2) G'nin öyle bir e elemanı vardır ki, G'deki herhangi bir a için

$acdot e=ecdot a=a$

eşitliği sağlanır (yani e etkisiz elemandır), ve de e, G'de bu özelliği sağlayan tek elemandır,

3) G'deki her a elemanı için öyle bir b elemanı bulmak mümkündür ki

$acdot b=bcdot a=e$

eşitliği sağlansın. Eğer bu eşitlik sağlanıyorsa b elemanına a elemanının tersi adı verilir.

Yukardaki tanımda dikkat edilmesi gereken bir nokta ise işlemimizin değişme özelliği olduğunu varsaymıyor oluşumuzdur. Yani bazı gruplarda öyle iki a ve b elemanı bulmak mümkündür ki $acdot bneq bcdot a$ olsun. Öte yandan eğer bir grupta fazladan değişme özelliği de varsa o gruba "Abel grubu" denir. Gruplar sonlu veya sonsuz sayıda eleman içerebilirler.

Gruplara bazı örnekler:

1) Tam sayılar kümesi ve üzerindeki toplama işlemi, bir Abel grubudur.

2) 0'dan farklı rasyonel sayılar ve çarpma işlemi, bu da Abeldir.

3) Simetrik n grubu, ${1,..., n}$ kümesinden kendi içersine birebir örten fonksiyonlardan oluşur. Eleman sayısı $n!$ dir ve Abel değildir.

4) Lie Grupları, Diferensiyel Geometri alanının uğraş konularıdır.

Kısa Tarih

İlk başta Fransız matematikçi Evariste Galois tarafından Cisimler Teorisi'ndeki sonlu genişlemeleri açıklamak için tanımlanmışlardır. Bu konu daha sonraları Galois genişlemeleri adıyla anılmaya başlanmış ve bu alanda karşımıza çıkan gruplara da Galois Grupları denmiştir. Galois grupları günümüzde hala daha Cebirsel Geometri alanının temel uğraş alanları içersindedirler. Öte yandan gruplar saf matematikte hızla başka uygulama alanları bulmuşlar ve Katı Hal Fiziği ve Oyunlar Teorisi gibi uygulamalı alanlara da sıçramışlardır. 1980'li yıllarda tamamlanan sonlu grupların sınıflandırılması projesi modern matematiğin en büyük başarılarından

Halka (matematik)

Halka, matematiğin temel yapılarından biridir ve soyut cebirde tam sayıların soyutlamasıdır. Bu yapıyı işleyen dala halka kuramı denir. Halkalara örnek olarak polinomlar, modülo n ya da karmaşık sayılar verilebilir.

Halka her şeyden önce bir kümedir ve belli özellikleri sağlar. Bu özellikler aşağıda verilmiştir.

Tanım [değiştir]

R boştan farklı bir küme olsun. Bu küme üzerinde "+" ve " $cdot$ " ikili işlemleri tanımlı olsun. Eğer;

(R,+) kümesi değişmeli bir öbek,
(R, $cdot$ ) kümesi bir yarı öbek ve
" $cdot$ " işlemi "+" işlemi üzerine sağdan ve soldan dağılmalı

ise (R,+, $cdot$ ) kümesine halka denir. Bunların yanında eğer,

(R, $cdot$ ) kümesi bir birlik ise (R,+, $cdot$ ) kümesine birimli halka; ayrıca,
(R, $cdot$ ) kümesi değişmeli ise (R,+, $cdot$ ) kümesine değişmeli halka denir.

Bir halkanın birinci işlemi olan (genellikle toplama) "+" işleminin birim öğesine sıfır denir ve 0 ile gösterilmesi gelenektir. Halkanın ikinci işlemi olan (genellikle çarpma) " $cdot$ " işleminin birim öğesi varsa bu birim öğeye bir denir ve geleneksel olarak 1 ile gösterilir.

Ayrıca bir halkada genellikle 0=1 olmadığı da bir belit olarak eklenir. Nitekim 1=0 olması bir çelişki yaratmaz ancak, 1=0 olduğunda R halkası tek öğeli bir küme olur. Bunu aşağıdaki gibi basitçe her sayının sıfıra eşit olduğunu göstererek kanıtlayabiliriz:

a = a.1 = a.0 = 0

Halkanın tam tanımı için bir uzlaşma görülmüyor. Bazı matematikçiler (örneğin Ali Nesin) bir halkanın hem birimli hem bileşmeli hem de değişmeli olduğunu varsayar^[1]. Eğer birim öğesiz veya değişme özelliği olmayan bir halkadan bahsedilecekse birimsiz halka ya da değişmesiz halka denmiş olur. Bourbaki ya da Herstein gibi matematikçiler de birim öğesi olmayan halkalara yalancı halka demeyi tercih eder. Bu sayfada bahsedilen halkalar hem değişmeli hem bileşmeli hem de birim öğeli alınacaktır

Topolojik uzaylar

Vikipedi, özgür ansiklopedi

(Topolojik Uzaylar sayfasından yönlendirildi)

Git ve: kullan, ara

Topolojik uzaylar, matematiğin Topoloji dalının başlıca uğraş konularıdır. Bir küme X ve bu kümenin alt kümelerinin bir kısmını içeren S kümesinden oluşurlar. S kümesinin aşağıdaki varsayımları sağlaması gereklidir.

1) $emptyset$ ve X kümeleri S'in elemanıdırlar,

2) S'in elemanları arasından seçilecek herhangi bir $U α$ kolleksiyonu alındığında, $bigcup_{alpha}U_{alpha}$ bileşim kümesi de S in bir elemanıdır,

3) S'in elemanları arasından seçtiğimiz $U 1,..., U n$ kümelerinin kesişimi olan $bigcap_{i=1}^n U_i$ kümesi de S'in elemanıdır.

Burada 2. şartta bahsettiğimiz koleksiyonun sonsuz sayıda eleman içerebileceğine ancak 3. şarttaki altkümelerin sayısının sonlu olduğuna dikkat etmek gereklidir.

Geleneksel olarak X in altkümelerinden S'in elemanı olanlara açık kümeler denir. Buna karşılık C kümesi X'in bir altkümesiyse ve de 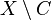$Xsetminus C$ fark kümesi açık bir kümeyse, o zaman C'ye de kapalı bir küme denir. Bu tanıma göre X ve $emptyset$ kümeleri aynı zamanda hem açık hem kapalıdırlar.

Diyelim ki verilen bir (X,S) topolojik uzayında X'in altkümelerinden oluşan öyle bir Y kümesi bulabiliyoruz ki her açık küme Y'nin elemanlarının bir bileşimi olarak yazılabiliyor, bu durumda Y kümesine (X,S) uzayının temeli denir.

Sıralamalar

Bir küme ve o küme üzerinde aşağıda tarif edilecek olan ikili bir ilişki içeren aksiyomatik sistemlere denir. Bilinen sıralama $leq$ ilişkisinin soyutlanmasıyla elde edilirler. Kümemize X, ilişkimize R adını verecek olursak, aşağıdaki aksiyomların sağlandığını varsayarız.

X kümesinin her a elemanı için R(a,a) ilişkisi sağlanmalıdır. ( $aleq a$ şeklinde düşünülebilir, yansıma özelliği olarak bilinir.)

X kümesinin herhangi iki a ve b elemanı için R(a,b) ve R(b,a) ilişkileri sağlanıyorsa, $a = b$ olamlıdır. (hem $aleq b$ hem de $bleq a$ sağlanıyorsa a=b dir diye düşünülebilir, antisimetrik olma özelliği olarak bilinir.)

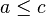X kümesinin herhangi üç a, b, ve c elemanı için hem R(a,b) hem de R(b,c) ilişkileri ağlanıyorsa, o zaman R(a,c) ilişkisi de sağlanmalıdır. (hem $aleq b$ hem de $bleq c$ ise $aleq c$ de olmalıdır diye de düşünülebilir, geçişkenlik özelliği olarak bilinir)

Sıralamalara Örnekler

(Doğal Sayılar, $leq$ ilişkisi) -- (Rasyonel Sayılar, $leq$ ilişkisi) -- (Reel Sayılar, $leq$ ilişkisi) -- (Kümeler Uzayı*, $subset$ ilişkisi)

$*$ Teknik olarak bir küme değildir ancak bu sorun yaratmaz.

Sıralama Çeşitleri

Eğer elimizdeki sıralama nesnesi, yukardaki aksiyomlara ek başka varsayımlar sağlamıyorsa elimizdeki sıralamaya "kısmi sıralama" denir. Yani her sıralama bir kısmi sıralamadır.

Eğer yukardaki aksiyomlara ek olarak X ten seçeceğimiz herhangi iki elemanı karşılaştırabiliyorsak (yani R(a,b) ve R(b,a) ilişkilerinden biri mutlaka doğru olmak zorundaysa) o zaman elimizdeki sıralamaya doğrusal sıralama denir. Yukardaki örneklerden (Doğal Sayılar, $leq$ ), (Rasyonel Sayılar, $leq$ ) ve (Reel Sayılar, $leq$ ) aynı zamanda doğrusal sıralamalara da örneklerken, (Kümeler Uzayı, $subset$ ilişkisi), doğrusal olmayan kısmi bir sıralamadır. Nedeni herhangi iki kümeyi $subset$ ilişkisine göre karşılaştırmanın mümkün olmamasıdır. Yani biri diğerini içermeyen iki kümenin varlığıdır.

Son olarak, doğrusal sıralama şartlarını sağlayan (X, R) sırlamalarından, "X in her alt kümesinin bir en küçük eleman içermesi şartı"nı sağlayanlara iyi-sıralama denir. Yukardaki örneklerden reel sayılar ve doğal sayılar iyi-sıralamalarken, rasyonel sayılar iyi sıralama değildir. Örnek olarak "karekök ikiden büyük rasyonel sayılar" kümesinin en küçük bir elemanı olmaması verilebilir.

Sıralamaların Önemi

Her sıralama nesnesi bir topolojik uzay yapısına sahiptir. Bu yapının açık kümelerinin temeli "öyle x elemanları ki 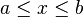$aleq xleq b$ " şeklinde ifade edilebilen kümelerden oluşur, a veya b az önceki formülde gözükmüyor da olabilirler.

Zorn'un Lemması, sayesinde kısmi sıralamalar matematiğin pek çok alanında uygulama bulmuşlardır. Mesela halka'larda maksimal ideallerin varlığı Zorn'un Lemması ve ideallarin $subset$ ilişkisine göre kısmi bir sıralama oluşturduğu gerçeği kullanılarak ispatlanır.

Reel Sayılar Kümesi'nin Rasyonel Sayılar Kümesi'ni kullanılarak oluşturulmasının bir temeli de Alman matematikçi Richard Dedekind tarafından verilmiştir. Dedekind'in yöntemi Rasyonel Sayılar Kümesi'nin bir iyi-sıralama haline getirilmesine dayanır. Diğer yöntem ise "bütünleme"dir.

İyi sıralamar matematikte nispeten nadir gözlenen, çok güçlü özellikler içeren objelerdir. Bu ilke ve kümeler teorisi arasındaki ilişki hakkında bilgi için ayrica İyi-sıralılık ilkesi Makalesi'ne bakabilirsiniz