Konuya matematikten değil de Türkçeden girelim. Fonksiyon kelimesinin öztürkçesi konusunda bir tartışma vardır. Kimi fonksiyonun öztürkçesi olarak "gönderme" sözcüğünü yeğlerken, kimi de doğrudan Frenkçeden çevirerek "işlev" sözcüğünü yeğlemektedir. Eğer sözcük seçiminin adlandırmak istenen şeyin anlamını tetiklemesini istiyorsak, bizce gönderme sözcüğü çok daha yerindedir, çünkü bir fonksiyon gerçekten de bir kümenin elemanlarını bir başka kümenin elemanlarına gönderir... Gönderme yerine - komiklik yapmak istiyorsak - götürme de diyebiliriz.

Önce fonksiyon kavramının sezgisel (ama olabildiğince matematiksel) anlamını verelim. A ve B iki küme olsun. A'nın her elemanını bir biçimde B'nin bir ve bir tek elemanıyla ilişkilendirelim. (Koyu renkle yazılmış sözcükler önemlidir; ilerde bunların üstünde duracağız.) Örneğin (gerçel sayılar kümesi), B de -3'ten büyük gerçel sayılar kümesi olsun, yani olsun. İlişkilendirmeyi de şöyle yapalım: A'nın her elemanını (yani her gerçel sayıyı), o elemanın karesiyle ilişkilendirelim. Böylece ilişkilendirmeyi bir formülle tanımlamış olduk. Bu örnekteki ilişkilendirmeyi olarak yazarız, her sayı karesiyle ilişkilendirilmiştir, örneğin -3 sayısı 9'la, sayısı 2'yle ilişkilendirilmiştir. İşte A'dan B'ye giden fonksiyon böyle bir şeydir. Daha simgesel olunur ve fonksiyon f gibi bir simgeyle ifade edilir. Verdiğimiz örnek için f(x) = x² yazılır.

Matematik dışından bir örnek verelim de sosyologlar da anlasın. A yaşamış ya da şu anda yaşayan insanlar kümesi olsun. f fonksiyonu her insanı annesine götürsün. Pek matematiksel olmasa da bu, A'dan A'ya giden bir fonksiyondur, çünkü her insanın bir annesi vardır (Adem babamızla Havva anamızı dikkate almayın bu örnekte). Ama her insanı kardeşine götüren bir fonksiyon yoktur çünkü bazı insanların kardeşi olmadığı gibi bazı insanların birden çok kardeşi vardır. Öte yandan, her insanı en büyük kardeşine götüren kural, kardeşi olan insanlar kümesinden A kümesine giden bir fonksiyondur.

Biraz daha matematiksel olalım. A'dan B'ye giden bir fonksiyonu, A kümesinin her elemanını B'nin bir ve bir tek elemanına götüren/elemanıyla ilişkilendiren bir "kural"dır. (Burada biraz yalan var, ama pek önemli değil: Kuralın ne demek olduğunu söylemediğimiz gibi, bir fonksiyonun tanımlanması için herhangi bir kurala da aslında gerek yoktur! İlerde, yazının sonunda, fonksiyonun gerçek matematiksel tanımını verdiğimizde bu pembe yalana ihtiyacımız kalmayacak.)

Özet olarak, verilmiş bir fonksiyonu, A'nın her elemanını bir biçimde B'nin bir ve bir tek elemanına götürür/elemanıyla ilişkilendirir.

Yukardaki örnekte, kural, f(x) = x² olarak verilmiştir. Ama bir fonksiyon bir formül ya da bir kuraldan öte bir şeydir. Bir fonksiyon, sadece bir kural değildir; bir fonksiyonu tanımlamak için, kural dışında, bir de ayrıca A ve B kümeleri de gerekmektedir. Formül ya da kural aynı kalsa bile A ve B kümeleri değişirse fonksiyon da değişir. Yukardaki örnek üzerinden gidelim:

Yukarda A = R ve almış ve fonksiyonu f(x) = x² kuralıyla tanımlamıştık. Şimdi A yerine alırsak ve formülü ve B kümesini aynı tutarsak, o zaman elde edilen fonksiyonunu gene f ile göstermek yanlış olur, çünkü bu iki fonksiyon değişik fonksiyonlardır. A₁'den B'ye giden ve kare alma kuralıyla tanımlanan fonksiyonu örneğin g ile gösterebiliriz.

Bunun gibi, B kümesi değişirse, o zaman fonksiyon da değişir; örneğin ise, kare alma kuralı A'dan B₁'e giden bir fonksiyon tanımlar ve bu fonksiyon, yukardakilerle karışmasın diye, f ya da g ile değil, bir başka simgeyle, örneğin h ile gösterilir.

Aynı şekilde A₁'den B₁'e giden bir fonksiyon, ya da h ile değil, örneğin k ile gösterilmelidir.

Yukarda koyu renkle yazdığımız sözcüklerin önemini açalım: Bir fonksiyonu, A kümesinin her elemanını B'nin bir elemanına götürür, yani A'nın bazı elemanlarını unutmuş olamaz. Örneğin, karekök alma kuralı, gerçel sayılar kümesi 'den 'ye giden bir fonksiyon tanımlamaz, çünkü negatif sayıların gerçel sayılarda karekökü yoktur. Ya da (doğal sayılar kümesi) ise, f(x) = x − 1 kuralı, A'dan B'ye giden bir fonksiyon tanımlamaz çünkü f(0) = − 1'dir ve olmasına karşın − 1 sayısı B'de değildir. Öte yandan bu f(x) = x − 1 kuralı, 'den tamsayılar kümesi 'ye giden bir fonksiyon tanımlar.

İkinci koyu renkli yere gelince... Bir fonksiyonu, A'nın her elemanını B'nin bir ve bir tek elemanına götürür, yani A'nın aynı elemanı B'nin iki ayrı elemanına gidemez. (Yukarda verilen kardeş örneğini anımsayın.) Örneğin ise, A'nin bir x elemanını x² = y² denkleminin y çözümlerine götüremez, çünkü eğer x = 0 değilse, bu denklemin R'de iki değişik y çözümü vardır, nitekim x² = y² denkleminin çözümleri y = x ve y = − x'tir. Burada, x'in x'e mi yoksa − x'e mi gideceği belirtilmemiştir ve bu, bir fonksiyon yaratmada sorun teşkil eder. Bir fonksiyonunda, A'nın her elemanını B'nin bir ve bir tek elemanına gitmelidir, iki ya da daha fazla elemana gidemez. (Birkaç yüzyıl önce bu tür fonksiyonlar kabul ediliyordu ama bugün bunlara fonksiyon denmiyor.)

Kalkış ve Varış Kümeleri.Bir fonksiyonunda, A'ya tanım kümesi ya da kalkış kümesi denir. B'ye de değer kümesi ya da varış kümesi denir.

Görüntü. Eğer ise f(x)'e x'in f altında görüntüsü adı verilir. B'nin

altkümesi f(A) olarak gösterilir ve bu kümeye f'nin görüntü kümesi adı verilir. (Kimi f(A) yerine B'ye görüntü kümesi demeyi yeğliyor ama bunun aldatıcı bir terim olduğunu düşünüyorum.)

Örneğin f(x) = x² kuralıyla tanımlanan f: (-3,5) R fonksiyonunun görüntü kümesi [0,25) aralıkıdır.

Fonksiyon Eşitliği. f ve g fonksiyonlarının birbirine eşit olması için, 1) tanım kümelerinin eşit olması, 2) değer kümelerinin eşit olması ve 3) tanım kümesindeki her x için f(x) = g(x) olması gerekmektedir. Bu üç koşuldan biri eksikse fonksiyonlar eşit olmaz. (Genellikle liselerde sadece üçüncü koşul üzerinde durulur.) Gene de eşitlikte en önemli koşul (3) koşuludur. Ardından (1) koşulu gelir. (2) koşulunun gözden kaçtığı olur.

Sabit Fonksiyonlar: A ve B iki küme olsun ve olsun. A'nı her elemanını B'nin bu b elemanına götüren fonksiyona sabit fonksiyon adı verilir. b değerini alan sabit fonksiyonu c_b olarak gösterirsek, o zaman fonksiyonu, her için c_b(x) = b kuralıyla tanımlanır. Not: A ve B kümelerinin önemini ortaya çıkarmak istiyorsak, c_b yerine c_b,A,B yazmak gerekebilir. Bu fonksiyona "sabit b fonksiyonu" adı verilir.

Bileşke mümkün olduğunda 'dir. Ama 'dir.

Eğer A ya da B'nin tek bir elemanı varsa, o zaman A'dan B'ye giden her fonksiyon sabit olmak zorundadır.

Eğlencelik. Eğer ve ise, A'dan B'ye giden bir fonksiyon yoktur.

Amatör matematikçilere tuhaf gelebilir belki ama eğer 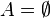ise, B hangi küme olursa olsun, A'dan B'ye giden bir ve bir tek fonksiyon vardır: boşfonksiyon... Pek de önemli olmayan bu olgu, birazdan, fonksiyonun matematiksel tanımı verdiğimizde bariz olacak.

Özdeşlik Fonksiyonu. Eğer A bir kümeyse, her için Id_A(x) = x kuralıyla tanımlanan Id fonksiyonuna A'nın özdeşlik fonksiyonu adı verilir. Özdeşlik fonksiyonu bileşkenin sağdan ve soldan etkisiz elemanıdır.

Bir Fonksiyonun Kısıtlanışı. Eğer bir fonksiyonsa ve , A'nın bir altkümesiyse, o zaman f fonksiyonunu A₁ altkümesine kısıtlayabiliriz, yani f'nin sadece A₁ kümesinin elemanlarında alacağı değerlerle ilgilenebiliriz. Bu yeni fonksiyon

olarak yazılır ve bu fonksiyona f'nin A₁'e kısıtlanmışı adı verilir. Elbette eğer ise eşitliği geçerlidir.

Varış Kümesini Değiştirmek. Bir fonksiyonun varış kümesini de değiştirebiliriz: bir fonksiyon olsun. B₁, f'nin görüntü kümesi f(A)'yı altküme olarak içeren herhangi bir küme olsun. O zaman A tanım kümesini ve f kuralını değiştirmeden yeni bir fonksiyonu elde edebiliriz. Bu fonksiyon - daha önceki paragraftaki gibi - özel bir simgeyle gösterilmez.

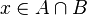Fonksiyonların Yapıştırılması ya da Birleşimi. ve iki fonksiyon olsun. A üzerinde f olan, B üzerinde g olan ve 'den V'ye giden bir fonksiyonu tanımlamak istiyoruz. Eğer ise hiç kuşku yok ki olmalı. Eğer ise gene hiç kuşku yok ki olmalı. Ama olduğunda, için f(x) ya da g(x) arasında bir seçim yapmalıyız, özellikle eğer ise... Bu durumda hangi seçimi yaparsak yapalım istediğimiz iki koşuldan birini çiğnemek zorunda kalacağız. Ama diyelim ki, her 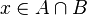için f(x) = g(x), yani f ve g fonksiyonları kesişiminde aldıkları değer aynı, bir başka deyişle . O zaman fonksiyonunu herhangi bir seçime gerek kalmadan şöyle tanimlayabiliriz:

eğer ise

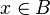eğer ise.

Bu fonksiyona f ve g fonksiyonlarının birleşimi ya da yapıştırılması adı verilir ve yukarda gösterildiği gibi bu fonksiyon olarak yazılır.

Örneğin fonksiyonu f(x) = x olarak tanımlanmışsa ve fonksiyonu g(x) = − x olarak tanımlanmışsa, o zaman fonksiyonu aynen mutlak değer fonksiyonudur: .

Elbette ve .

Gene elbette diye bir fonksiyon varsa diye bir fonksiyon da vardır ve bu iki fonksiyon birbirine eşittir.

Yukardaki yapıştırmayı yapabilmemiz için f ve g fonksiyonlarının varış kümeleri aynı olmak zorunda değildi. Nitekim, eğer ve iki fonksiyon ise ve bu fonksiyonların kümesinde aldıkları değer eşitse, o zaman A üzerinde f olan, B üzerinde g olan bir fonksiyonunu gene tanımlayabiliriz.

İkiden çok, hatta sonsuz tane fonksiyonu da yapıştırabiliriz eğer gerekli koşullar sağlanıyorsa: bir fonksiyon ailesi olsun. Ayrıca her göstergeçleri (endisleri) için f_i ve f_j fonksiyonlarının kesişiminde aldıkları değerler eşit olsun. O zaman her 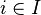ve her için eşitliğini sağlayan bir fonksiyonu,

"eğer ise "

kuralıyla tanımlanabilir. Bu tür yapıştırmalar topolojide ve analizde sık sık kullanılır.

Bir Fonksiyonun Altkümeler Kümesinde Neden Olduğu Fonksiyon. bir fonksiyon olsun. A'nın her X altkümesi için, B'nin f(X) altkümesi şöyle tanımlanır:

.

Bu f(X) yazılımı ender de olsa soruna yol açabilir, çünkü A'nın X altkümesi bal gibi de aynı zamanda A'nın bir elemanı olabilir, o zaman f(X) ifadesinin fonksiyonunun X'te aldığı değer mi olduğu, yoksa yukardaki gibi B'nin altkümesi olarak mı tanımlandığı anlaşılamaz. Örneğin, A = {0,{0}} olsun. B = {5,6} olsun. fonksiyonu, f(0) = 5, f({0}) = 6 olarak tanımlansın. Ve son olarak X = {0} olsun. X, hem A'nın bir elemanı hem de bir altkümesidir. X eleman olarak görüldüğünde f(X) = 6 olur ama altküme olarak görüldüğünde f(X) = {5} olur. Belki bu yüzden

tanımı yerine,

tanımını yapmak daha yerinde olur.

Eğer P(X), X'in altkümeleri kümesiyse, yukardaki 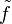kuralı, P(X)'ten P(Y)'ye giden bir fonksiyon tanımlar. Bu 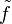fonksiyonu altküme olma ilişkisine saygı duyar.

Fonksiyonun Matematiksel Tanımı. Nihayet fonksiyonun matematiksel yani biçimsel yani teorik tanımını verelim. A ve B iki küme olsun. F, 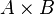kartezyen çarpımının şu özelliği sağlayan bir altkümesi olsun:

Her için, ilişkisini sağlayan

bir ve bir tane elemanı vardır.

Bu durumda üçlüsüne fonksiyon adı verilir. İki tanım daha: A, fonksiyonunun tanım kümesidir, B ise varış kümesidir.

fonksiyonuna f adını verirsek, verilen bir için B'nin ilişkisini sağlayan yegane y elemanı f(x) olarak gösterilir. Kimi zaman f(x) yerine fx yazıldığı da olur. Demek ki, her için olur. Ayrıca F kümesine f fonksiyonunun grafiki adı verilir.

Fonksiyonu matematiksel olarak tanımlamak için "kural"dan hiç sözetmediğimize dikkatinizi çekeriz. Ama F'nin bir küme olması gerektiği canalıcı noktadır. Ama bu canalıcı nokta mantıkçılar dışında kimseye canalıcı gelmez.

Eğer 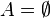ise üçlüsünün bir fonksiyon olması için F'nin boşküme olması gerektiği açıktır, işte bu üçlüsü boşfonksiyondur.

İlgili maddeler:

Birebir fonksiyon

Örten Fonksiyon

Eşleme

Eşleşme

Seçim Fonksiyonu

Daha önceki arkadaşın yazdıkları bir iki düzeltmeyle aşağıda.

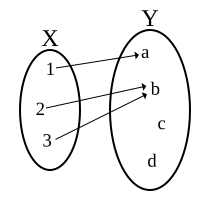
X kümesindeki her eleman (bir giriş) , Y kümesindeki bir elemanla mutlaka eşlenmelidir. (bir çıkış)

 

Bu gösterim bir işlev (fonksiyon) değildir. (Bir girişe iki çıkış vardır.)

 

Örnek bir işlev (fonksiyon) grafiği

Gönderme Örnekleri

• Doğal sayılarda bir sayının ardılı bir göndermedir.

• İki dğeişkenli göndermeler de vardır.

• Verilen sıraya karşılık gelen çift sayıyı söyleyen bağıntı bir göndermedir: f(n)=2n.
• Bir küme üzerinde tanımlı bir ikili işlem, göndermedir: f(x,y)=x+y.
• Diziler birer göndermedir.

için yani

Tanım [değiştir]

A'dan B'ye tanımlı bir gönderme (f), (A,B,F) şeklinde gösterilebilen bir üçlüdür. Burada F, aşağıdaki özelliklere sahip sıralı ikili kümesidir.

Başka bir deyişle, bir bağıntının gönderme olabilmesi için, A kümesindeki herhangi bir öğenin B kümesinden en fazla bir öğeyle eşleşmesi gerekmektedir.

Gönderme, daha soyut matematiksel anlamda bir kümedir ve tanımı şu şekildedir: 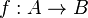göndermesi için,

buradaki simgesi y nin biricik olduğunu ifade eder.

Yukarıdaki resmi tanımlama, her zaman kullanışlı olmadığından genelde göndermeler farklı tanımlanır.

En yaygın tanımlama biçimi, örneklerde görüldüğü gibi sağ tarafı girdilere (parametrelere) dayalı formül, sol tarafı göndermenin ve bağımsız girdilerin belirtildiği bir eşitliktir.

Göndermeler aşağıda örnekte görüldüğü gibi parçalı şekilde de tanımlanabilir.

Tümevarımla yakın ilişkisi olan ilginç bir tanımlama biçimi de yinelgedir. Örneğin Fibonacci Serisi'nin üretici göndermesi şu şekilde tanımlanabilir.

Boylece 'den 'ye giden bir fonksiyonu tanımlanır.

Göndermelerin Kümesel Özellikleri [değiştir]

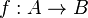şeklinde tanımlı bir gönderme,

• Birebir ise, A kümesinde tanımlı olduğu her değeri B kümesinden ayrı bir öğeye eşler,
• İçine ise B kümesinde, eşlenmemiş en az bir değer vardır,
• Örten ise A kümesindeki bütün öğeler için tanımlıdır.